Как можно регрессировать ряды нисходящих трендов в Excel?
Я хотел бы использовать эти данные для получения уравнения с использованием Excel.
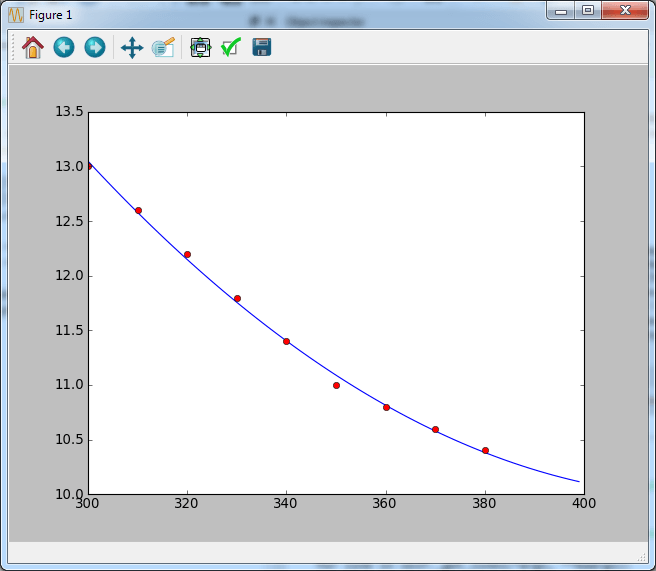
300 13
310 12.6
320 12.2
330 11.8
340 11.4
350 11
360 10.8
370 10.6
380 10.4
Когда х идет вверх, у идет вниз. Кажется, просто. Но когда я делаю полиномиальную регрессию на этих данных, даже если линия тренда очень хорошо соответствует данным, генерируемое ею уравнение не работает. Уравнение 0.0096x2 - 0.4181x + 13.341 Когда я добавляю значения x к этому уравнению, числа увеличиваются! Так что здесь что-то не так.
Мои шаги:
- поместите обе серии номеров в Excel
- выберите второй набор (13, 12,6 ...)
- построить линейный график
- установить первый набор в качестве меток оси X
- выберите Series1 и добавьте полиномиальную (2) линию тренда, отобразите уравнение, отобразите R-квадрат
Это приводит к приведенному выше уравнению со значением R^2.9955. Но когда я использую это уравнение, он не производит эти выходные данные для этих входов.
Очевидно, я делаю что-то не так.
Изменить: или это Excel? Вот график этого уравнения (выше): 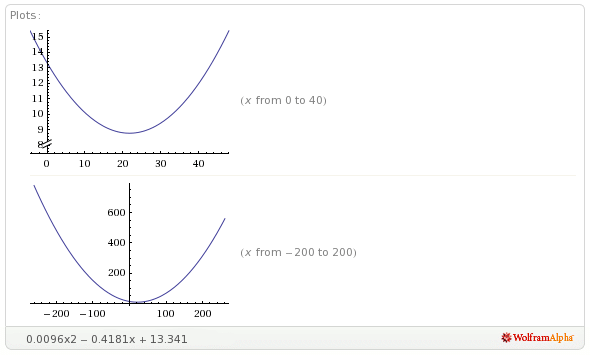
Очевидно, что это не имеет тенденцию к снижению в диапазоне 300-390.
Вот реальное уравнение, которое соответствует этим данным:
Квадратичное соответствие: y=a+bx+cx^2 Данные коэффициента:
а = 4,53Е +01 б = -1,66Е-01 с = 1,95Е-04
Спасибо CurveExpert 1.4.
2 ответа
Я не знаю, как вы получили это уравнение в Excel, так как это уравнение, которое я получаю:
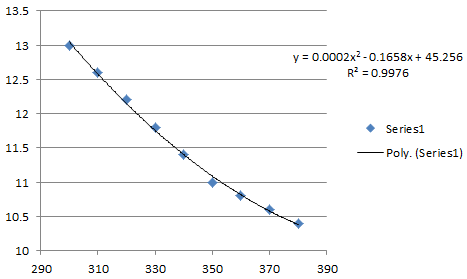
Убедитесь, что степень полинома равна 2, и что вы не установили никаких перехватов или прогнозов при создании линии тренда.
Другое дело, вы сказали, х увеличивается, а у уменьшается. Это означает, что вы должны выполнить экспоненциальную подгонку кривой (если только это не линейное уменьшение, которого нет):
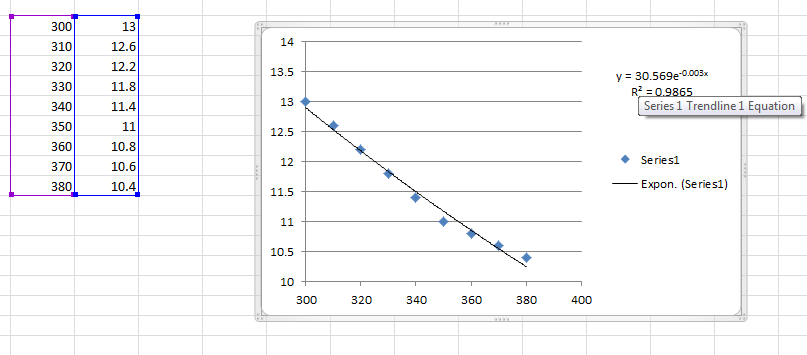
Важно отметить, что подгонка кривой действительно работает только в пределах введенных вами данных. Вы не можете точно "предсказать" будущие значения, используя это. Вы можете только оценить значения между границами ваших исходных данных.
Причина, по которой я предлагаю использовать экспоненту, связана с пониманием "тренда" данных и того, как компьютеры рассчитывают эти "уравнения тренда". Например, предположим, у меня есть 3 точки данных, и я создаю полиномиальную функцию, которая идеально подходит для данных:
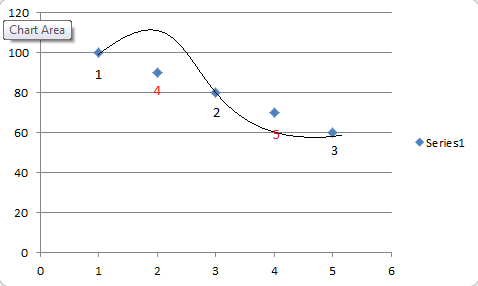
Однако, когда я беру больше точек данных, они лежат вне того, что соответствуют моим исходным точкам данных (Да, я понимаю, что Excel НИКОГДА не будет выполнять подобную функцию, но стоит подчеркнуть это). При анализе данных необходимо принять какое-то решение на основе того, что они знают.
Несмотря на то, что мое значение R ниже, чем ваше (всего на 0,01) знание того, что данные уменьшаются с увеличением x, делает экспоненциальный лучший выбор из-за того, что вы УЖЕ знаете. Так же, как линейная подгонка будет лучшим выбором на графике выше. Это основное различие между экстраполяцией и интерполяцией.
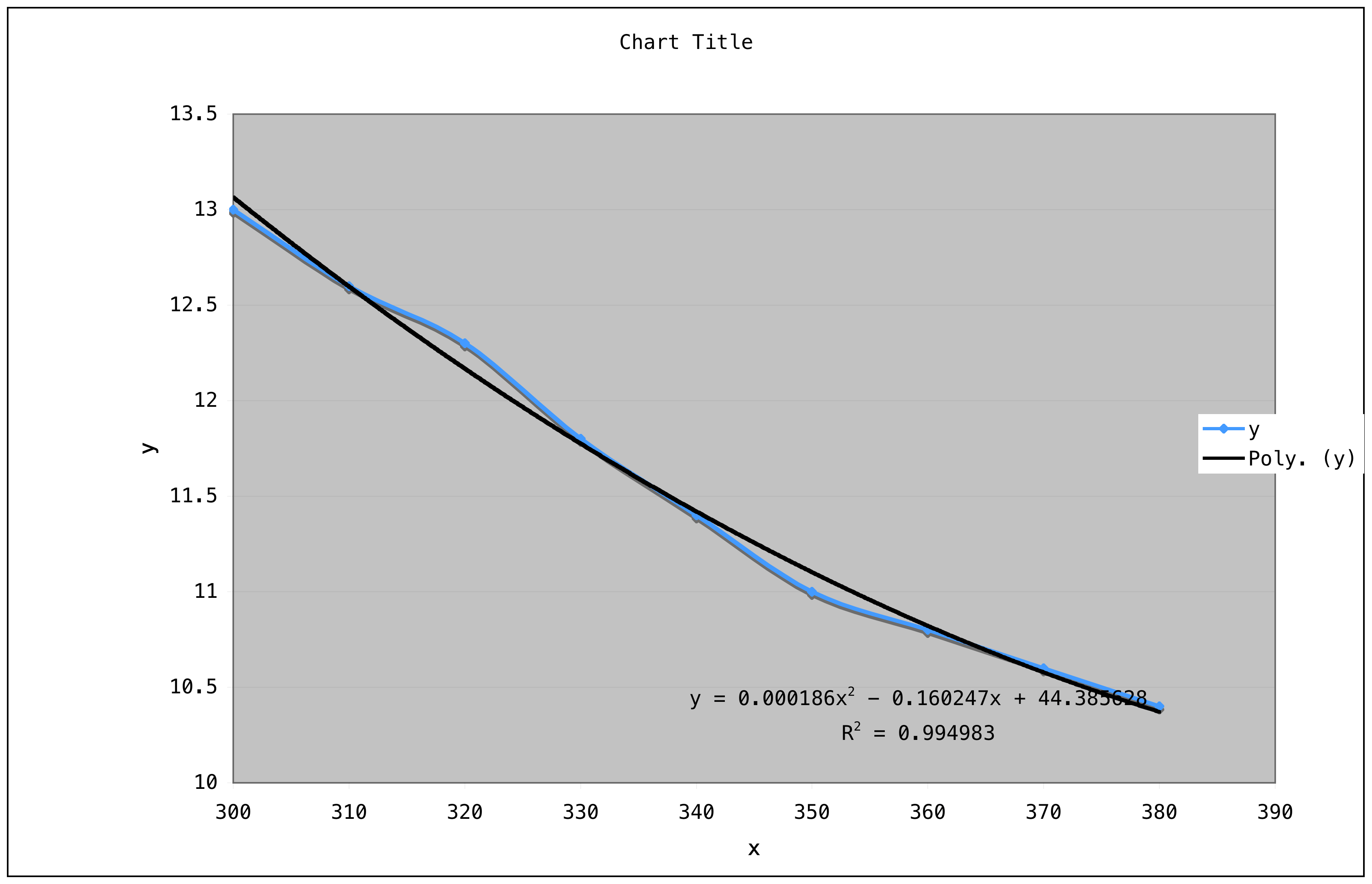
Я вошел в них и получил результат как
y = .000186x^2 - 0,160247x + 44,385628 с R^2 = 0,995
так хорошо подходит
Я ввел х и у в качестве заголовков столбцов
Тогда первый столбец был значения х, а второй столбец у
Выберите оба столбца
Вставить диаграмму - ось скрипки
Добавьте линию тренда.